รางวัลโนเบลสาขาฟิสิกส์ 2024

การประกาศรางวัลโนเบลสาขาฟิสิกส์ประจำปี 2024 ได้สร้างความตื่นเต้นพร้อมๆกับความประหลาดใจให้กับหลายๆคนไม่น้อย เมื่อราชบัณฑิตยสภาด้านวิทยาศาสตร์แห่งสวีเดน (The Royal Swedish Academy of Sciences) ได้ตัดสินใจมอบรางวัลโนเบลสาขาฟิสิกส์ประจำปี 2024 ให้กับ จอห์น เจ ฮอปฟิลด์ (John J. Hopfield) และ เจฟฟรีย์ อี ฮินตัน (Geoffrey E. Hinton) สำหรับการค้นพบและการเชื่อมแนวคิดฟิสิกส์พื้นฐานที่ช่วยวางรากฐานให้กับการพัฒนาเครือข่ายประสาทเทียม (Artificial Neural Networks – ANNs) ซึ่งเป็นหนึ่งในเทคนิคที่สำคัญของการพัฒนาระบบการเรียนรู้ของเครื่อง (machine learning) ที่สำคัญอย่างยิ่งในปัจจุบัน กล่าวคือ งานวิจัยที่ทางด้านปัญญาประดิษฐ์ (Artificial Intelligence; AI) น่าจะเป็นงานวิจัยในสาขาคอมพิวเตอร์มากกว่าที่จะเป็นงานวิจัยในสาขาฟิสิกส์ อย่างไรก็ตาม เมื่อพิจารณาในเชิงลึกเกี่ยวกับขั้นตอนวิธี (algorithm) ที่ขับเคลื่อนการคำนวณเครือข่ายประสาทเทียมในปัจจุบันจะพบว่ามีความเชื่อมโยงกับฟิสิกส์สถิติ (statistical physics) อย่างลึกซึ้ง คำถามที่ตามมา คือ เครือข่ายประสาทเทียมคืออะไรและฟิสิกส์สถิติเข้ามามีส่วนร่วมในการคำนวณในเครือข่ายประสาทเทียมได้อย่างไร

เครือข่ายประสาทเทียมคืออะไร?

เครือข่ายประสาทเทียมเป็นแบบจำลองทางคณิตศาสตร์ในคอมพิวเตอร์ ที่ได้รับแรงบันดาลใจจากการทำงานของสมองมนุษย์ โดยเครือข่ายเหล่านี้ประกอบด้วยชั้นของโหนด (nodes) ที่ดำเนินการจัดการข้อมูล โหนดทั้งหลายในเครือข่ายจะเชื่อมต่อกันผ่านการถ่วงน้ำหนัก (weighted connections) คล้ายกับการเชื่อมต่อของเซลล์ประสาทในสมอง เครือข่ายประสาทเทียมจะเรียนรู้ด้วยการปรับการน้ำหนักการเชื่อมต่อระหว่างโหนดเหล่านี้จากข้อมูลชุดฝึกฝน (training datasets) หลายๆแบบเพื่อเตรียมเครือข่ายที่พร้อมสำหรับการให้คำตอบในภายหลัง (พิจารณารูปที่ 1) ลักษณะเช่นนี้แตกต่างจากการทำงานในโปรแกรมคอมพิวเตอร์ทั่วไปที่ทำตามคำสั่งแบบเป็นขั้นตอนที่มีกฎเกณฑ์แบบกำหนดไว้ตายตัวก่อนหน้า

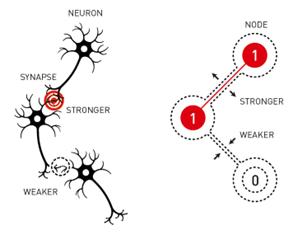
รูปที่ 1: แสดงการเชื่อมโยงระหว่างเซลล์ประสาทในสมองจริงและเซลล์ประสาทเทียมที่เชื่อมต่อกันด้วยการถ่วงน้ำหนัก (ที่มา : Popular information. NobelPrize.org. Nobel Prize Outreach AB 2024. Wed. 9 Oct 2024. https://www.nobelprize.org/prizes/physics/2024/popular-information/ )

แม้ว่าเครือข่ายประสาทเทียมจะมีศักยภาพสูง แต่ในช่วงเริ่มต้นของการพัฒนากลับพบข้อจำกัดสำคัญเกี่ยวกับการทำให้เครือข่าย “เรียนรู้” ได้อย่างมีประสิทธิภาพ เช่น ในช่วงทศวรรษที่ 1960 ขั้นตอนวิธีเพอร์เซ็ปตรอนแบบหลายชั้น (multi-layer perceptron) ที่พัฒนาขึ้นไม่สามารถแก้ไขปัญหาที่ซับซ้อน (โดยเฉพาะกับปัญหาแบบไม่เชิงเส้นหรือปัญหาข้อมูลที่มีสัญญาณรบกวนสูง) ได้อย่างมีประสิทธิภาพเท่าที่ต้องการ ปัญหานี้ทำให้นักวิจัยหลายคนในช่วงนั้นเชื่อว่าการพัฒนาเครือข่ายประสาทเทียมน่าจะถึงทางตันและอาจจะไม่สามารถนำไปใช้ในงานที่ซับซ้อนได้อย่างมีประสิทธิภาพ

การค้นพบของฮอปฟิลด์: แนวทางฟิสิกส์สู่การเรียนรู้จดจำ

ในปี ค.ศ. 1982 จอห์น เจ ฮอปฟิลด์ นักฟิสิกส์ผู้มีความสนใจในระบบชีววิทยา ได้เสนอแนวคิดที่สำคัญที่ถือได้ว่าเป็นการปฏิวัติวงการเครือข่ายประสาทด้วยการสร้างเครือข่ายฮอปฟิลด์ (Hopfield Network) แนวคิดนี้ใช้หลักการจากระบบสปิน (spin system) และการลดพลังงานในทางฟิสิกส์เพื่อแก้ปัญหาการจดจำรูปแบบ (pattern recognition)  โดยสามารถเก็บคุณลักษณะของรูปแบบข้อมูลไว้ในเครือข่ายประสาท

แนวคิดที่สำคัญและโดดเด่นในงานของฮอปฟิลด์ คือ การพิจารณาการเรียนรู้ของเครือข่ายโดยอาศัย เงื่อนไขการลดพลังงาน (energy minimization) ให้ต่ำสุด คล้ายกับระบบทางกายภาพที่อุณหภูมิคงที่ที่จะพยายามปรับตัวเข้าสู่สถานะที่มีพลังงานต่ำที่สุดเพื่อเข้าสู่สภาวะเสถียร ในเครือข่ายฮอปฟิลด์นี้ ตัวแปรพลังงานนี้จะใช้เป็นตัวชี้วัดความถูกต้องหรือประสิทธิภาพในกระบวนการรู้เรียนเพื่อจำแนกข้อมูลซึ่งสถานะที่มีพลังงานต่ำจะแสดงถึงการจำแนกที่ถูกต้องหรือแม่นยำ ในขณะที่สถานะที่มีพลังงานสูงจะแสดงถึงการจำแนกที่ผิดพลาดหรือความไม่แน่นอน ในขณะที่เครือข่ายประมวลผลข้อมูลจะทำปรับตนเองเพื่อลดพลังงานโดยมีเป้าหมายเพื่อเข้าสู่สถานะพลังงานต่ำที่สอดคล้องกับความทรงจำที่เก็บไว้(หรือคำตอบที่ถูกต้อง) ดังนั้น เมื่อทำการส่งข้อมูลนำเข้าในรูปแบบที่ไม่สมบูรณ์หรือมีสัญญาณรบกวนให้กับระบบเครือข่าย ระบบจะทำการจำแนกผ่านการคำนวณโดยใช้น้ำหนักระหว่างโหนดเพื่อค้นหาลักษณะรูปแบบที่จำไว้ที่มีลักษณะใกล้เคียงสอดคล้องกับรูปแบบที่นำเข้ามากที่สุด กล่าวคือระบบจะเริ่มต้นจากสถานะข้อมูลที่มีรูปแบบไม่สมบูรณ์นั้น แล้วเคลื่อนที่ไปในภูมิทัศน์พลังงานที่มีทั้งเนินและหลุมบ่อและไปสิ้นสุดในสถานะที่เสถียร(คำตอบ)ที่เรียนรู้ไว้ก่อนหน้าดังแสดงในรูปที่ 2

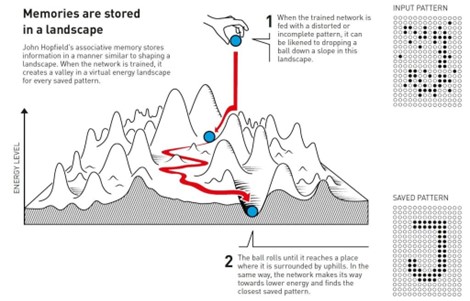
รูปที่ 2: แสดงภาพจำลองภูมิทัศน์พลังงานในเครือข่ายฮอปฟิลที่เมื่อได้รับรูปแบบข้อมูลที่ไม่สมบูรณ์หรือมีสัญญาณรบกวน เครือข่ายจะปรับตนเองเพื่อลดพลังงานในการนำระบบไปสู่หุบเขาที่ใกล้ที่สุด ซึ่งสอดคล้องกับรูปแบบที่จดจำไว้ กระบวนการนี้เปรียบได้กับการที่ลูกบอลกลิ้งลงจากเนินเพื่อค้นหาสถานะพลังงานที่ต่ำที่สุดและเรียกคืนรูปแบบที่เสถียร (ที่มา : Popular information. NobelPrize.org. Nobel Prize Outreach AB 2024. Wed. 9 Oct 2024. https://www.nobelprize.org/prizes/physics/2024/popular-information/ )

ฟิสิกส์เบื้องหลังเครือข่ายฮอปฟิลด์ สามารถอธิบายได้โดยอาศัยสมการพลังงาน E ของเครือข่ายซึ่งมีนิยามในลักษณะ

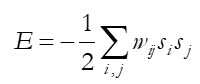
โดยที่ w_ij​ แทนค่าถ่วงน้ำหนักระหว่างเซลล์ประสาทโหนด i และ j และ s_i​ และ s_j​ คือ สถานะไบนารี (0 หรือ 1) ของเซลล์ประสาทโหนดที่ i และ j  สถานะไบนารีนี้คล้ายกับสถานะของอนุภาคแม่เหล็กในวัสดุที่วางตัวในหนึ่งๆหรือทิศทางตรงข้ามในแกนที่กำหนด การเชื่อมต่อระหว่างโหนดผ่านการถ่วงน้ำหนักนี้เรียกว่าการถ่วงน้ำหนักซินแนปส์ (synaptic weights) ซึ่งจะถูกปรับค่าตามกฎการเรียนรู้ของเฮบบ์ (Hebbian learning) ที่ว่า “เซลล์ประสาทที่ถูกกระตุ้นพร้อมกันจะเชื่อมต่อกันอย่างเข้มแข็ง” กฎนี้ได้รับแรงบันดาลใจจากผลงานของนักประสาทวิทยาที่ชื่อว่าโดนัลด์ เฮบบ์ ทั้งนี้จะเห็นได้ว่าสมการนี้คล้ายกับสมการฮามิลโทเนียนในแบบจำลองไอซิง (Ising model) ในฟิสิกส์สถิติ ที่กลุ่มของสปินจะพยายามลดพลังงานโดยรวมของระบบเพื่อเข้าสู่สภาวะที่เสถียรผ่านการจัดเรียงทิศทางในรูปแบบต่างๆ  และโดยการนำแนวคิดนี้มาใช้ฮอปฟิลด์จึงสามารถสร้างเครือข่ายที่เก็บข้อมูลในลักษณะที่มีความเสถียรได้ ซึ่งเป็นการปฏิวัติแนวทางจัดเก็บและเรียกคืนข้อมูลในเครือข่ายประสาท

อย่างไรก็ตาม แม้ว่าเครือข่ายฮอปฟิลด์จะเป็นที่ยอมรับอย่างกว้างขวางแต่ยังมีข้อจำกัดอยู่ เช่น ในบางครั้ง เครือข่ายอาจติดอยู่ในสถานะพลังงานต่ำเฉพาะที่ (local minima) ซึ่งเป็นหุบเขาเล็กๆ ในภูมิทัศน์พลังงานที่ไม่ใช่คำตอบที่ถูกต้องที่เป็นสถานะพลังงานต่ำทั่วไป (global minima) นอกจากนี้ เครือข่ายยังมีลักษณะคำตอบเฉพาะ(ตามที่กำหนดไว้ในขั้นตอนการเรียนรู้) จึงขาดอิสระในการสร้างรูปแบบคำตอบใหม่ที่ตอบสนองแบบพลวัตรกับผู้ใช้

กระบวนทัศน์ของฮินตัน: การก้าวข้ามข้อจำกัดด้วยเครื่องโบลต์ซมันน์

ในช่วงกลางทศวรรษที่ 1980 เจฟฟรีย์ ฮินตัน ได้ต่อยอดผลงานของฮอปฟิลด์ โดยพัฒนาเครื่องโบลต์ซมันน์ (Boltzmann Machine) ซึ่งเป็นเครือข่ายประสาทที่สามารถเรียนรู้ได้อย่างยืดหยุ่นโดยอาศัยหลักความน่าจะเป็น ที่นำเสนอโดยนักฟิสิกส์ที่ชื่อว่า ลุดวิก โบลต์ซมันน์ (Ludwig Boltzmann)  เครื่องโบลต์ซมันน์ใช้การจำลองความผันผวนทาง “ความร้อน” (“thermal” fluctuations) ระหว่างการเรียนรู้ในการเปลี่ยนแปลงคุณลักษณะของเครือข่ายแบบเฟ้นสุ่ม (stochastic) ในการสร้างรูปแบบต่างๆของเครือข่ายได้อย่างอิสระภายใต้เงื่อนไขความน่าจะเป็นที่กำหนด กล่าวคือ เครื่องโบลต์ซมันน์ทำงานโดยการปรับน้ำหนักของเครือข่ายตามการแจกแจงความน่าจะเป็นของชุดข้อมูลที่ได้รับโดยใช้สมการการแจกแจงความน่าจะเป็นของโบลต์ซมันน์ (Boltzmann’s probability distribution function) ในเครื่องโบลต์ซมันน์นี้การกำหนดความน่าจะเป็นหรือโอกาสที่เครือข่ายจะอยู่ในสถานะใดสถานะหนึ่งจะขึ้นอยู่กับพลังงานของสถานะนั้น คือ

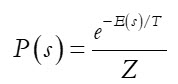
โดยที่ P(s) คือความน่าจะเป็นที่เครือข่ายจะอยู่ในสถานะ s , E(s) คือพลังงานของสถานะ s, T คือพารามิเตอร์อุณหภูมิ(หน่วยไม่เจาะจง)ที่ควบคุมระดับของการสุ่ม และ Z คือ ตัวแปรบรรทัดฐาน (ทำหน้าที่ในลักษณะเดียวกันกับฟังก์ชันพาร์ทิชัน, partition function) ที่ทำให้ผลรวมของความน่าจะเป็นทั้งหมดเท่ากับ 1

จากคุณลักษณะของเครื่องโบลต์ซมันน์นี้ จึงทำให้สามารถเรียนรู้รูปแบบใหม่และสามารถสร้างรูปแบบใหม่ได้จากข้อมูลที่เคยฝึกมาก่อน ซึ่งให้ความยืดหยุ่นและความสามารถในการสร้างสรรค์ให้กับเครือข่าย (โดยการอุปมา อาจจะพิจารณาคำตอบที่ได้จากแบบจำลองภาษาใหญ่ เช่น ChatGPT หรือ Gemini ที่แตกต่างกันแม้จะถามด้วยคำถามเดิม และสามารถปรับอุณหภูมิในข้อความพร้อมรับเพื่อให้ได้คำตอบที่มีลักษณะตรงเป้าหมายตายตัวหรือมีลักษณะสร้างสรรค์มากยิ่งขึ้นได้) ผลที่ตามมาเครื่องโบลต์ซมันน์ได้กลายมาเป็นรากฐานของการพัฒนาการเรียนรู้เชิงลึก (deep learning) ด้วยเทคนิคต่างๆ (เช่น การเบี่ยงเบนแบบเปรียบเทียบ (contrastive divergence) และการฝึกเครือข่ายแบบชั้นต่อชั้นโดยใช้ restricted Boltzmann machines (RBMs)) ที่ช่วยให้การฝึกเครือข่ายเชิงลึกซึ่งเคยเป็นปัญหาที่ยากมากในอดีตให้เป็นไปได้ อันช่วยยังประโยชน์ต่อการประยุกต์ใช้ด้านต่างๆไม่ว่าจะเป็นการพัฒนาการวิจัยทางด้านวิทยาศาสตร์(เช่น การค้นพบอนุภาคฮิกซ์ การค้นพบดาวเคราะห์ต่างระบบ การสืบสร้างภาพหลุมดำ) รถยนต์ขับเคลื่อนอัตโนมัติ การประมวลผลภาษา และแม้กระทั่งแบบจำลองปัญญาประดิษฐ์เชิงสร้างสรรค์ (Generative AI) เช่น ChatGPT หรือ DALL·E เป็นต้น

ด้วยเหตุนี้ จึงถือได้ว่าผลงานของ จอห์น เจ ฮอปฟิลด์ และ เจฟฟรีย์ อี ฮินตัน ได้ช่วยพัฒนาศักยภาพของเครือข่ายประสาทเทียมและการเรียนรู้ด้วยเครื่องจากการแก้ปัญหาพื้นฐานในทางทฤษฎีไปสู่เครื่องมืออันทรงพลังที่ขับเคลื่อนโลกในปัจจุบันด้วยการใช้แนวคิดจากฟิสิกส์สถิติ ผลงานของพวกเขาได้วางรากฐานให้กับเทคโนโลยีปัญญาประดิษฐ์สมัยใหม่ที่ปฏิวัติเทคโนโลยีในอุตสาหกรรมต่างๆอย่างหลากหลาย รางวัลโนเบลสาขาฟิสิกส์ประจำปี 2024 จึงเป็นการยกย่องผลงานของฮอปฟิลด์และฮินตันและตระหนักถึงความเชื่อมโยงที่ลึกซึ้งระหว่างความรู้ทางฟิสิกส์และระบบปัญญาประดิษฐ์ ที่ช่วยขับเคลื่อนโลกและมีผลกระทบสูงต่อรูปแบบการใช้ชีวิตของมนุษย์ในปัจจุบัน

รายละเอียดเพิ่มเติม

• The Nobel Prize in Physics 2024 Press release. NobelPrize.org. <https://www.nobelprize.org/prizes/physics/2024/press-release/>
• Popular science background: They used physics to find patterns in information. org. <https://www.nobelprize.org/uploads/2024/10/popular-physicsprize2024-2.pdf>
• Scientific background: “For foundational discoveries and inventions that enable machine learning with artificial neural networks”. NobelPrize.org. <https://www.nobelprize.org/uploads/2024/09/advanced-physicsprize2024.pdf>

ผู้เขียน: รองศาสตราจารย์ ดร.ยงยุทธ เหล่าศิริถาวร